Veri madenciliğinde farklı yöntemler kullanılmaktadır. Kullanılan yöntemler problem türüne göre, elde bulunan veriye göre ve uygulama alanına göre farklılıklar gösterebilmektedir. Kullanılan yöntemlerin birçoğu yapay zekânın alanıdır. Veri madenciliğinde kullanılan yöntemler temel olarak ‘Öngörü Yöntemler’ ve ‘Tanımlayıcı Yöntemler’ temel olarak 2’ye ayrılmaktadır. Öngörü yöntemleri ‘Sınıflandırma’ ve ‘Regresyon’ olarak alt modellere ayrılmaktadır. Tanımlayıcı yöntemler ise temel olarak ‘Kümeleme’ ve ‘Birliktelik Kuralları’ olarak alt modellere ayrılmaktadır. Veri madenciliğinde kullanılan yöntemlerin ayrıntılı gösterimi Şekil 1’de mevcuttur.
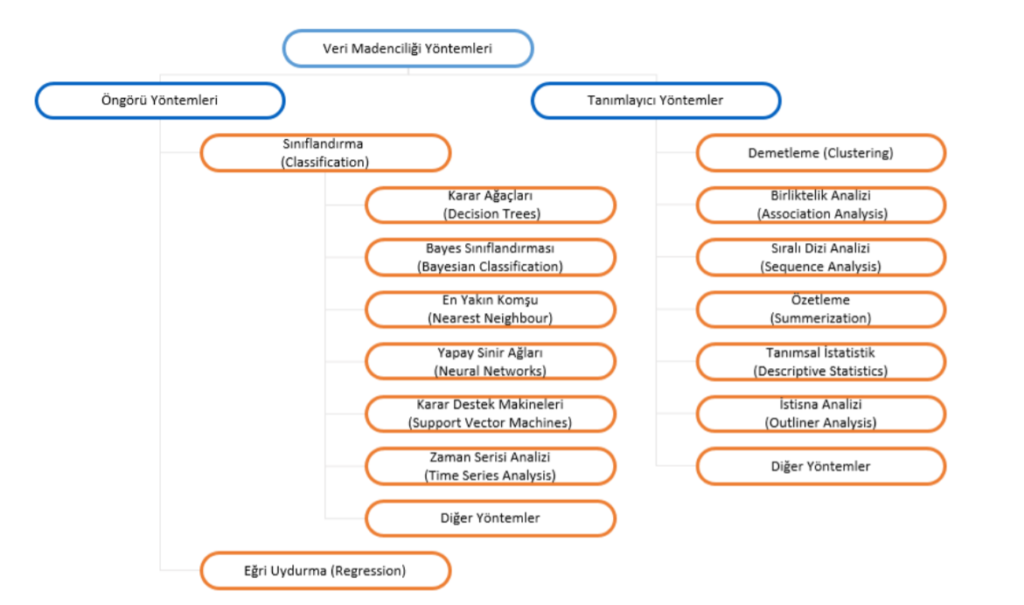
Şekil 1: Veri Madenciliği Yöntemleri [1]
- Sınıflandırma
Sınıflandırma, en sık uygulanan veri madenciliği tekniğidir. Öğrenmede eğitim verileri sınıflandırma algoritması ile analiz edilir. Sınıflandırmada, test verileri, sınıflandırma kurallarının doğruluğunu tahmin etmek için kullanılır. Doğruluk kabul edilebilir ise yeni veri demetlerine kurallar uygulanabilir. Sınıflandırıcı eğitim algoritması, doğru ayrımcılık için gerekli olan parametre setini belirlemek için bu önceden sınıflandırılmış örnekleri kullanır. Algoritma daha sonra bu parametreleri bir sınıflandırıcı olarak adlandırılan bir modele kodlamaktadır [2].
Sınıflandırma Modellerinin Türleri:
- Karar Ağaçları
- Bayes Sınıflandırma
- En yakın Komşu
- Yapay Sinir Ağları
- Karar Destek Makineleri
- Zaman Serisi Analizi
2. Regresyon
Regresyon çözümlemesi, bir bağımlı değişkenin başka bağımsız değişkenlere olan bağımlılığını, bağımlı değişkenin ana kütle ortalama değerini, bağımsız değişkenin yinelenen örneklerdeki bilinen ya da değişmeyen değerleri cinsinden tahmin etme ve/veya kestirme amacı ile incelemektedir [5].
3.Kümeleme/Demetleme
Kümeleme analizinin kullanılmasında benzer uzaklıklar dikkate alınarak yararlanılabilecek alternatif ölçü ve yöntemler bulunmaktadır. Kümeleme algoritması veritabanını alt kümelere ayırır. Her bir kümede yer alan elemanlar dâhil oldukları grubu diğer gruplardan ayıran ortak özelliklere sahiptir. Kümeleme modellerinde amaç, Şekil 2’ de görüldüğü gibi küme üyelerinin birbirlerine çok benzediği, ancak özellikleri birbirlerinden çok farklı olan kümelerin bulunması ve veri tabanındaki kayıtların bu farklı kümelere bölünmesidir [3].
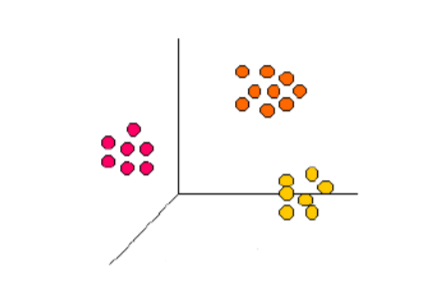
Şekil 2. Koordinat Düzleminde Kümeleme Örneği [3]
4. Biriktelik Kuralı
Birliktelik kuralı madenciliği, tüm sık geçen öğelerin bulunması ve sık geçen bu öğelerden güçlü birliktelik kurallarının üretilmesi olmak üzere iki aşamalıdır. Birliktelik kuralının ilk aşaması için kullanılan Apriori Algoritması, sık geçen öğeler madenciliğinde kullanılan en popüler ve klasik algoritmadır. Bu algoritmada özellikler ve veri, Boolean ilişki kuralları ile değerlendirilir [4]. Birliktelik kuralı uygulamasına pazar sepeti analizi örnek verilebilir (Frawley vd., 1991). Birliktelik kuralındaki amaç; alışveriş esnasında müşterilerin satın aldıkları ürünler arasındaki birliktelik ilişkisini bulmak, bu ilişki verisi doğrultusunda müşterilerin satın alma alışkanlıklarını tespit etmektir. Satıcılar, keşfedilen bu birliktelik bağıntıları ve alışkanlıklar sayesi ile etkili ve kazançlı pazarlama ve satış imkanına sahip olmaktadırlar [6].
KAYNAKÇA
[1] Albayrak, M. (2017). Bilimsel araştırmalarda veri madenciliği kullanımı. IJSSER, 3(3), 752-756.
[2] https://www.kadirblog.com/veri-madenciligi-algoritmalari-ve-teknikleri/
[3] Sariman, G. (2011). Veri madenciliğinde kümeleme teknikleri üzerine bir çalışma: k-means ve k-medoids kümeleme algoritmalarının karşılaştırılması. Süleyman Demirel Üniversitesi Fen Bilimleri Enstitüsü Dergisi, 15(3), 192-202.
[4] Özçakır, F. C., & Çamurcu, A. Y. (2007). Birliktelik kuralı yöntemi için bir veri madenciliği yazılımı tasarımı ve uygulaması.
[5] Damodar N. Gujarati, Temel Ekonometri, İstanbul, Literatür Yayınları, 2001, s. 16.
[6] https://www.veribilimiokulu.com/associationrulesanalysis/
