Daha önceki yazımızda “Kovaryans Analizi” ile ilgili genel bilgileri öğrenmiştik. Bu yazımızda analizin nasıl uygulandığını öğrenerek SPSS ile bir örnek çözeceğiz. Keyifli okumalar…
Uygulama Aşamaları
1-Öncelikle regresyon prosedürü uygulanır.
2-Daha sonra da düzeltilmiş değerler üzerinden normal varyans analizi yöntemi uygulanır. Böylelikle, bağımlı değişken ile ortak değişken arasındaki doğrusal ilişki için bir düzeltme yapılmış olur ve sonucunda hata varyansı düşer, veriler arasındaki diğer farklılıklar göz önüne alınarak grup farklılıkları ortaya konulabilir.
Frigon ve Laurencelle’nin (1993) ANCOVA analizi yapmak için hazırlamış olduğu basamaklar:
1. Basamak: Öncelikle ANCOVA varsayımlarından biri olan bağımsız değişkenin gruplarındaki regresyon eğimlerin homojenliği test edilir. F-testi yardımıyla test edilen bu durumda p <0,05 çıktığı durumlarda istatistiksel anlamlılık bulunur ve gruplar içi regresyon eğimleri homojendir.
2. Basamak: Bağımlı değişken ile kovaryant değişken arasında doğrusal bir ilişkinin varlığı incelenir.
3. Basamak: Bağımlı değişken ile kovaryant değişken arasında doğrusal bir ilişki bulunmaz ise doğrusal olmayan ANCOVA gibi farklı tekniklere yönlenilmelidir. Eğer doğrusal ilişki ortaya çıkmış ise ANCOVA uygulanarak grupların düzeltilmiş ortalamaları arasındaki fark olup olmadığı incelenmelidir.
4. Basamak: Ortak değişkene göre düzenlenmiş grup ortalamaları farkları istatistiksel olarak anlamlı çıktığı durumlarda üç ya da daha fazla grubun karşılaştırılması için post-hoc (çoklu karşılaştırma) testlerine başvurulur.
Kovaryans analizinde kullanılan analiz yöntemleri ve formüller:
Kovaryans: İki değişkenin birbirleri ile olan ilişkisini gösterir. Aşağıdaki şekilde hesaplanır:

Sonuç 0’dan büyükse pozitif ilişki, 0’dan küçükse negatif ilişki 0 ise ilişki yok demektir.
Korelasyon: İki değişkenin birbirine ne kadar benzerlikte hareket ettiğini gösterir. Aşağıdaki şekilde hesaplanır:

Sonuçlar 1 ile -1 arasında sonuç alır. Korelasyon katsayısı 1’e ne kadar yakınsa bağ o kadar kuvvetlidir.
0 ise herhangi bir bağdan bahsedilemez.
Regresyon Analizi: Geçmiş verilere dayanarak iki değişken arasındaki ilişkiyi tanımlamak amacıyla kullanılır. Aşağıdaki şekilde hesaplanır:

a ve b değerleri hesaplandıktan sonra y=a+b.x formülünden doğru oluşturulur.
Test İstatistiği: Varyans analizinde temel amaç, ikiden fazla örnek için X(i) ortalamalarının genel ortalamadan sapmalarının kareler toplamını, bu sapmalara sebep olan unsurlar itibariyle kısımlara ayırmak ve analiz etmektir. Bu analiz sonunda, örnekler arasında uygunluk olup olmadığı yani söz konusu örneklerin aynı anakütleye ait birer şans örneği olup olmadıkları da ortaya konulmuş olur.
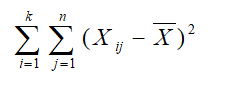
Eşitliğin sol tarafındaki ifadeye genel kareler toplamı (GKT) denir. Eşitliğin sağ kısmındaki ifadelerin birincisi örnek ortalamalarının genel ortalamadan gösterdiği sapmalar, diğeri ise her bir örnekteki değerlerin kendi örnek ortalamalarından gösterdiği sapmalardır. Birincisine, gruplar arası kareler toplamı (GAKT), ikincisine grup içi kareler toplamı (GİKT) denir.
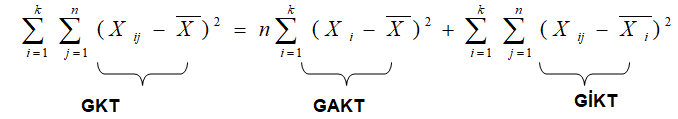
Gruplar arası serbestlik derecesi (df) = n-1
n: grup sayısı
Gruplar içi serbestlik derecesi (df) = n-2
n: örnek sayısı
Gruplar arası kareler ortalaması s₁², gruplar içi kareler ortalaması s₂² bölünerek varyans analizinin test istatistiği olan F değeri elde edilir.
Uygulama
Depresyonu azaltma yönünde uygulanan iki tedavinden hangisinin hastalar üzerinde daha etkili olduğu tespit edilmek isteniliyor.
Gönüllüler tedaviyi aldıktan sonra depresyon seviyeleri ölçülüyor ve not alınıyor.
Ancak gönüllülerin tedaviyi almak için geldikleri günlerde bazen hava çok kapalı bazen ise güneşlidir. Hepimizin bildiği üzere havanın kapalı veya açık olması mutluluğu etkilemektedir.
Gerçekten tedavinin kişiler üzerindeki etkilerini gözlemleyebilmek için hava durumu verilerini ortadan kaldırmak gerekmektedir.
Örneğimiz için kullanılan veriler aşağıda verilmiştir.
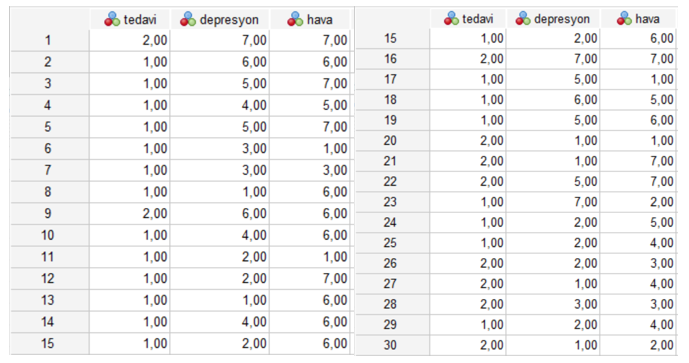
Homojenlik (regresyon eğrilerinin) varsayımının sağlanabilmesi için bu değerin 0.05 den büyük olması gerekir.
Bu varsayımı sağladığımız için örneğimize devam ediyoruz.
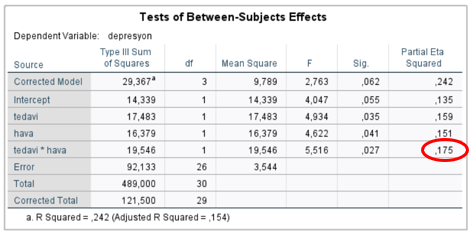
Bu tablo bize varyanslarımızın homojen dağılıp dağılmadığını gösterir.
Bu değer 0.05 ten büyükse bu varsayımın sağlandığını küçükse sağlanamadığını gösterir.

Peki gerçekten bizim havanın depresyon da etkisi var mı?
Eğer Sig. Değeri (anlamlılık düzeyi) 0.05 ten büyükse bu sorunun cevabı evettir.
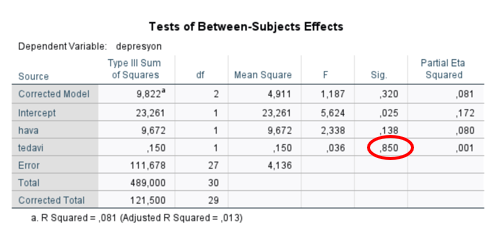
Bu tablodan yola çıkarak havanın da kontrol edildiği bir analizde 1 nolu tedavinin 2 nolu tedaviye göre daha başarılı olduğunu söyleyebiliriz.
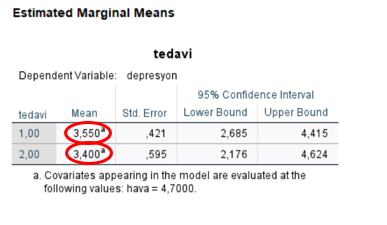
Bilgiyle kalın..
Kaynakça
- SPSS ile ANCOVA analizi ve Hipotez Testleri | Akademi Link
- https://dergipark.org.tr/en/download/article-file/1050184
- http://www.pbsciences.org/fulltext/8-1470811929.pdf?1637423594
